近日,数学系李常品教授团队及其合作者在《Chaos》上发表题为“Fractional SEIR Model and Data-Driven Predictions of COVID-19 Dynamics of Omicron Variant”的研究论文,该工作以特色展示论文(Featured Articles)的形式快速发表(Fast Track),并被American Institute of Physics (AIP)亮点报道(Scilight),认为“蔡等人开发了一种改进的流行病学模型,用于描述和预测这种变体的传播。”此项工作由金沙威尼斯欢乐娱人城李常品教授团队和美国工程院院士、布朗大学应用数学系George Em Karniadakis教授合作完成,金沙威尼斯欢乐娱人城数学系青年教师蔡敏为第一作者,李常品教授为论文唯一通讯作者,金沙威尼斯欢乐娱人城为第一署名单位和通讯单位。
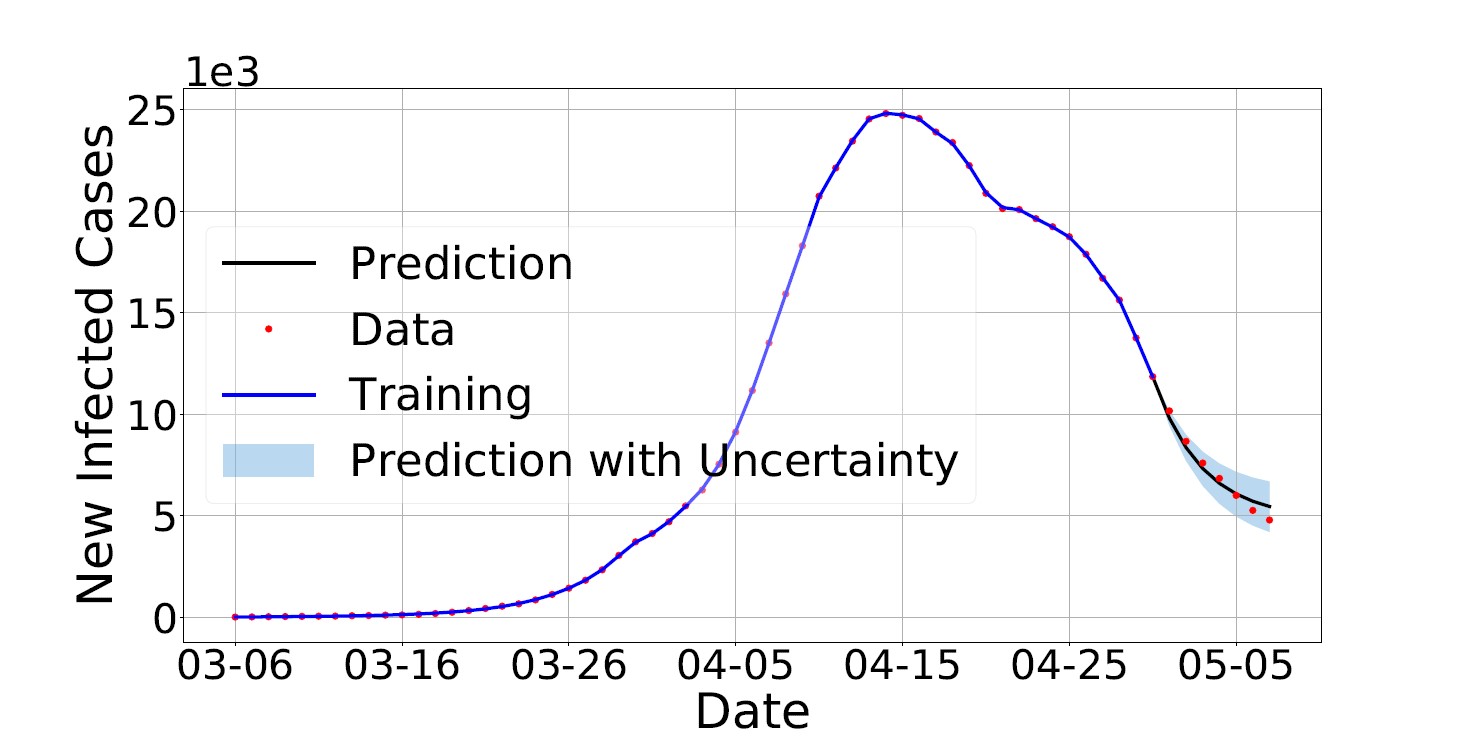
以阿达马分数阶微积分(Hadamard fractional calculus)为基础建立的洛姆尼茨对数蠕变律(Lomnitz logarithmic creep law)非常适合描述超慢过程(ultra slow process)。作者基于对实际数据的观察,建立了Caputo-Hadamard型分数阶SEIR模型,用于描述和预测Omicron病毒的传播。运用物理信息神经网络求解分数阶SEIR模型的反问题,推断出未观测到数据的状态变量、常数形式的模型参数以及函数形式的模型参数,进而应用校准后的模型进行预测。通过与实际数据对比表明,校准后的模型可以给出非常可信的预测。该项工作展现了基于物理信息神经网络的深度学习框架在分数阶微分方程模型中的应用潜能,为分数阶微分方程正、反问题的求解提供了新思路。
近些年来,李常品教授团队在Caputo-Hadamard型分数阶偏微分方程建模、分析、计算方面做出了有意义的工作,发表了10余篇文章。这些工作发表在非线性科学领域的权威期刊、ASME汇刊、以及科学计算领域的高级别期刊上,如: Journal of Nonlinear Science、Journal of Computational and Nonlinear Dynamics、 Journal of Scientific Computing等。
上述工作得到了国家自然科学基金和金沙威尼斯欢乐娱人城的大力支持。
论文链接:https://aip.scitation.org/doi/10.1063/5.0099450
Featured Articles链接:https://aip.scitation.org/topic/collections/featured?SeriesKey=cha
Scilight链接:https://aip.scitation.org/doi/10.1063/10.0012847